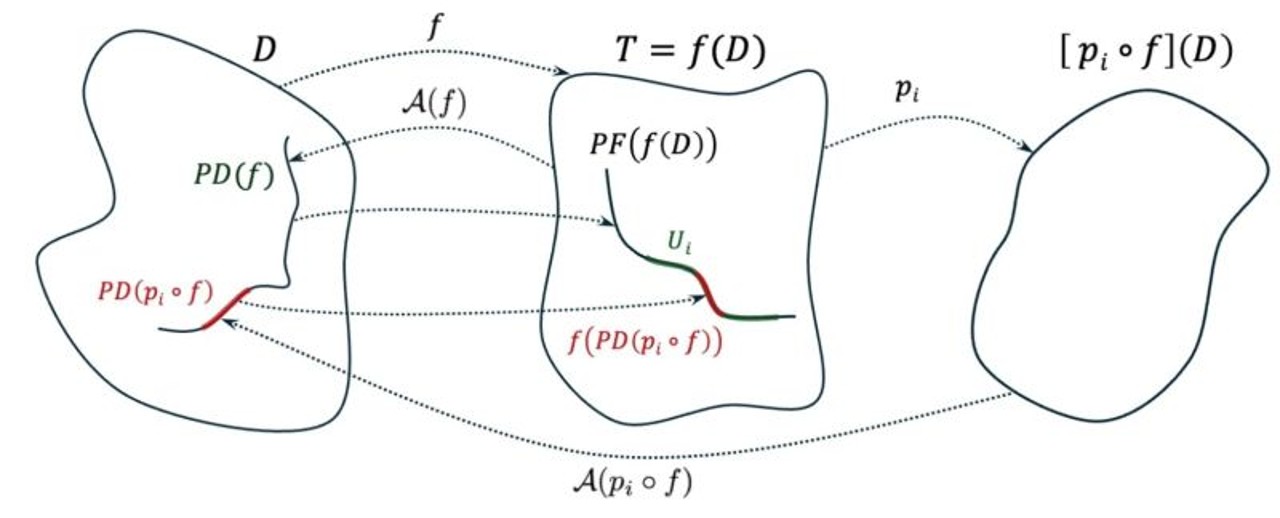
Multi-criteria decision-making requires understanding trade-offs between conflicting objectives. Multi-objective optimization (MOO) provides this through the Pareto optimal solutions. We introduce a mathematical framework to customize MOO algorithms to individual needs, based on composing black-box functions with support functions that maintain Pareto points. We prove the fundamental structures of support functions, deriving construction rules such as edge point identification. This methodology offers two advantages: classifying and tailoring MOO algorithms to desired Pareto front search attributes, and expanding their applicability significantly.

Find the paper here.