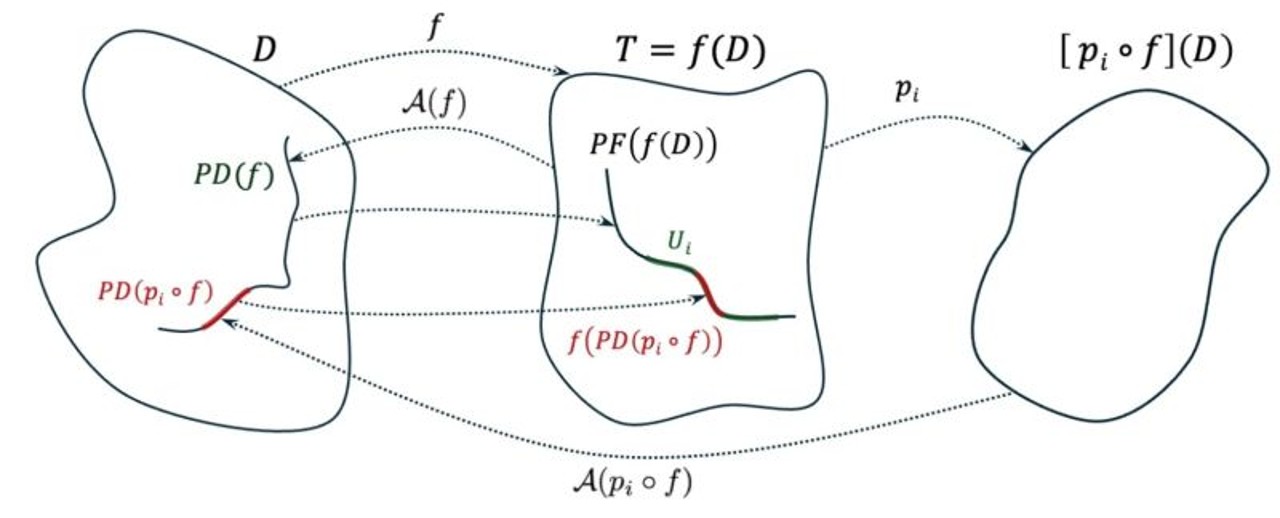
Auf das Problem zugeschnittene Konstruktion eines Algorithmus zur multikriteriellen Optimierung durch Pareto-Reflexionen
Bei der Multi-Kriterien-Entscheidungsfindung sind Kenntnisse über Kompromisse zwischen widersprüchlichen Zielen notwendig. Die Multi-Objektiv-Optimierung (MOO) liefert diese Informationen durch Pareto-optimale Lösungen. Wir stellen ein mathematisches Rahmenwerk vor, das MOO-Algorithmen an individuelle Bedürfnisse anpasst. Es basiert auf der Kombination von Black-Box-Funktionen mit maßgeschneiderten Unterstützungsfunktionen, die Pareto-Punkte bewahren müssen. Wir beweisen mathematisch die grundlegenden Strukturen der Unterstützungsfunktionen und leiten daraus Konstruktionsregeln ab. Diese Methode bringt zwei Hauptvorteile: die Möglichkeit, MOO-Algorithmen nach Pareto-Front-Suchattributen zu klassifizieren und anzupassen, sowie die Erweiterung des Anwendungsbereichs von MOO-Algorithmen.
Hier finden Sie das Paper.